 rechts oben, wenn Ihr zum Ausgangsfenster zurückkehren wollt!
rechts oben, wenn Ihr zum Ausgangsfenster zurückkehren wollt!
 Nora ist in einer Turnabteilung mit 30 Kindern. Der
Altersunterschied des jüngsten und des ältesten Kindes beträgt 5 Jahre.
Wie viele Kinder haben mindestens im gleichen Jahr Geburtstag? Wie viele
Kinder haben mindestens im gleichen Monat Geburtstag?
Nora ist in einer Turnabteilung mit 30 Kindern. Der
Altersunterschied des jüngsten und des ältesten Kindes beträgt 5 Jahre.
Wie viele Kinder haben mindestens im gleichen Jahr Geburtstag? Wie viele
Kinder haben mindestens im gleichen Monat Geburtstag?
 Es geht weiter mit der Uhr. Kann man das Ziffernblatt einer
Uhr so in 6 Teile zerlegen, dass sich in jedem Teil 2 Zahlen befinden
und die Summe der beiden Zahlen in allen 6 Teilen gleich groß ist?
Es geht weiter mit der Uhr. Kann man das Ziffernblatt einer
Uhr so in 6 Teile zerlegen, dass sich in jedem Teil 2 Zahlen befinden
und die Summe der beiden Zahlen in allen 6 Teilen gleich groß ist?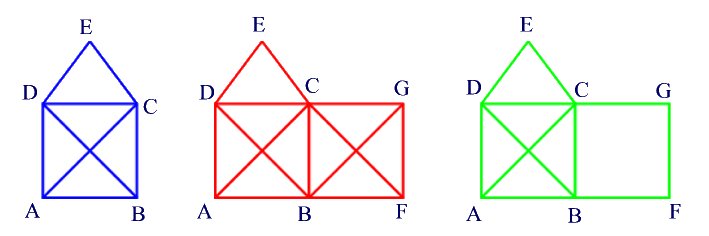
 Die Osterhasen besitzen zum Eierkochen eine Sanduhr, die 3 Minuten
läuft und eine Sanduhr, die 7 Minuten läuft. Wie können sie damit einen
Zeitraum von 8 Minuten messen?
Die Osterhasen besitzen zum Eierkochen eine Sanduhr, die 3 Minuten
läuft und eine Sanduhr, die 7 Minuten läuft. Wie können sie damit einen
Zeitraum von 8 Minuten messen? Unterteile die nebenstehende Fläche in 3 gleich große und
kongruente Teilflächen.
Unterteile die nebenstehende Fläche in 3 gleich große und
kongruente Teilflächen.
Flächen sind dann kongruent, wenn sie nach dem Ausschneiden genau (flächendeckend) aufeinander passen.
 In der Osterhasenschule steht die nebenstehende Aufgabe an der
Tafel. Dabei stehen gleiche Buchstaben für gleiche Ziffern. Wie lautet
die entsprechende Zahlenaufgabe?
In der Osterhasenschule steht die nebenstehende Aufgabe an der
Tafel. Dabei stehen gleiche Buchstaben für gleiche Ziffern. Wie lautet
die entsprechende Zahlenaufgabe?